The Inverse of Fun

The other night, my wife and I were talking and laughing about things that were fun and not fun.  I uttered the phrase, "the inverse of fun," and my wife said, "The inverse of fun would be one-over-fun."  We laughed even more as I pictured the expression for the inverse of fun in my head:  1/fun.

I was laughing because my wife was correct.  As a math teacher, though, I decided to be more precise.  So I told her that the multiplicative inverse of fun is indeed 1/fun.  But what if fun were a function?  Then the term "inverse" would mean something else entirely.

That was a concept I had been working through that very week.  You may recall from my previous blog posts (apologies for not posting for so many months; I haven't been able to find time for exploring fractals) that I adapted a small Java program to generate and explore various fractal equations.  There was one fractal, the so-called "Mandeldrop," that I desperately wanted to explore.  I first ran into it here, where the author of the page states it is an "inverted" Mandelbrot set.  I really liked the picture, but without any more details about the Mandeldrop's generation, I had to puzzle out the precise meaning of "inverted."

I found a forum that said that the Mandeldrop maps the complex number z to 1/z.  That is exactly the definition of inverse that my wife provided.  However, when I tried to code it that way, the results were garbage.  I realized I needed to understand more about complex numbers.

To date in this project, I have learned a lot (and shared a lot) about complex numbers.  But they are so, well, complex that I hadn't yet considered what the inverse of a complex number would look like.  However, right in the middle of wikipedia's page on complex numbers, previously studied, is the equation that describes the inverse of a complex number.  It took me a while to translate the equation into usable code, but by the time I did, the results were still less than satisfactory.

So I considered the idea that the Mandelbrot set is actually a function.  So what is the inverse of this function?  I puzzled it out and translated it into code.  But the results were so far off I decided that I was now barking up the wrong tree.  I had to go back to the inverse of a complex number and figure out how to apply it to the Mandelbrot equation.

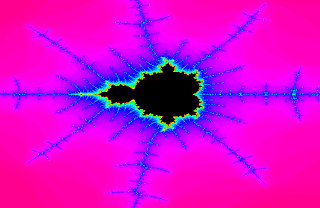
You may recall that the Mandelbrot set is generated by iterating the equation z = z^2 + c, where z = c at the start.  We take a point on the complex plane, square it and add the original point.  We take that answer, square it and add the original point.  Then we take the new answer, square it and add the original point.  We do this many times (which is why it can only done by computers) for every point on the screen.  If the point trends toward infinity, we give it a color; if it sticks around near the starting point, we leave it black.

When I finally realized I needed to invert both z and c, I got the Mandeldrop set.

This image has been rotated 90 degrees so the "drop" part of its shape is more evident.  Look at this basic Mandelbrot set that has been rotated, for comparison:

Can you see the part of the Mandelbrot set that is pointing straight up?  It looks like the Space Needle.  You can see this in the Mandeldrop.  Look at the bottom of the drop, the large circle there.  It's similar in shape and structure to the circle at the top of the Mandelbrot set, but if you look closely, you can see the "Space Needle" as well.  Let me provide you with a close up:

This close up proves that what the Mandeldrop set does, as the inverse of Mandelbrot, is turn the Mandelbrot set inside out.  Need more proof?  Let's zoom in on the top of the Space Needle.

It's a tiny Mandelbrot set, hidden in the Mandeldrop.  Naturally, there are uncountable numbers of tiny Mandelbrots in the Mandeldrop.

The thing I like about Mandeldrop is visually it reminds me of standing on the floor of a canyon as the sun is at the horizon; you look up and the sky is bright, but the walls of the canyon are black.  

Eureka 

A couple days after successfully generating the Mandeldrop, I had a moment of inspiration (if I can be so bold as to call it that).  From my previous blogs, you'll recall how the Mandelbrot set morphs when you modify the basic equation from z^2+c to z^3+c to z^4+c.  Well, I wondered, what would happen if you did the same to the Mandeldrop?  The result wasn't what I expected, so take a moment and think about how it'll change. 

OK, ready?  Here is the Cubic Mandeldrop:

It has two points.  Note the large circles at 12 and 6 o'clock have two "antennae", just as the Cubic Mandelbrot does.

Here is the Quartic Mandeldrop:

Once again, there are similarities between the Quartic Mandelbrot and this.  You can scroll down and look at previous posts to see what they are.

Before I go, I want to share one of the better mistakes...

While trying to find the inverse of the Mandelbrot set, I tried various configurations.  Most of them were garbage, but there was one fractal that was slightly interesting.  Below I show a close up of the one near-miss I had.  The tips at 12 and 6 o'clock seem to touch the rest of the fractal.  I zoomed in on the conjunction point to see if they actually touched or not, but I zoomed and zoomed and zoomed and never came up with a definitive answer.  Interesting, isn't it?

Mandelbrot on Steroids

If you've read (and remembered) my earlier posts, the Mandelbrot set is generated by iterating the complex number z with the equation z^2 + c.  Have you ever wondered what effect the power of two has on the set?  In other words, what if we pumped up the Mandelbrot and iterated z^3 + c?

You would find what is called the Cubic Mandelbrot.  (The original Mandelbrot is considered Quadratic.)  Picture please!

You can see the some parts of the Quadratic Mandelbrot and doubled in the Cubic Mandelbrot.  I like how the bulbs on the top and bottom (and smaller bulb clones on the sides) look like insect antennae.

OK, let's zoom in:

The "antennae" continue on forever, and have little Cubic Mandelbrots in them!  To wit:

Let's look at some close ups with different coloring:

This last one looks a little bent from the original.  I'm not sure what causes it, but I have seen distortions in other fractals like that when zooming up close.

Here are a few more of the Cubic Mandelbrot before I move on.  I like how these look like tropical islands.  Note the self-similarity at varying scales even at this extreme close-up.

Just as there's a Cubic Mandelbrot, there is also a Cubic Mandelbar.  Some examples:

 Interestingly, while the Cubic Mandelbrot has two bulbs, the Cubic Mandelbar has four arms.  But you should also notice the "antennae" at the end of each arm.  Zooming in on one (and changing the color scheme):

 Up close, it looks a lot like the Cubic Mandelbrot (except for the tiny Cubic Mandelbars on the antennae).

Zooming in even more,

 we find tiny Cubic Mandelbrots inside the Cubic Mandelbar.  Considering the same thing happens in the Quadratic Mandelbrot/Mandelbar, this is not surprising.  But it remains fascinating.

So what happens if we amp up the Cubics into Quartics?  Good question:

Quartic Mandelbrot

Note that instead of two "antennae" on each bulb, now there are three.

Quartic Mandelbar

Again, there are three "antennae" on each arm.  Some closeups:

Tiny Quartic Mandelbar

Tiny Quartic Mandelbrot

A distorted Quartic Mandelbrot

Quartic Mandelbar with Quartic Mandelbrot in it

Mandelbrot's Cousin -- The Mandelbar

Despite the intricate complexities of the Mandelbrot set, one can start to become less interested in it after awhile.  Fortunately for those who appreciate new territories, there are other fractal sets to explore.  The obvious first choice to explore is the Mandelbar Set (also called "Tricorn").  I say it's obvious because it's closely related to Mandelbrot, but for you to understand its relation, we have to talk a little math first.

Actually, let's let wikipedia tell us.  I choose wikipedia as a reference because it has the most words.  I mean, it has more examples in easy-to-understand language.  It even explains where the term "Mandelbar" comes from.  So without further ado, here are wikipedia's entries for complex conjugates and Mandelbar.

Since a picture is worth a thousand wikipedia articles, here are a few pictures of Mandelbar that I generated.

This is the basic Mandelbar.  You can see why fractal artists also call this the Tricorn.  The smooth parts near the center are not as interesting as the rough parts on the points.  

This miniature Mandelbar is located to the left of the figure above.  This example of self-similarity confirms that the Tricorn is indeed a fractal in the same ways the parent fractal, Mandelbrot is.  In fact, if you look closely, you will find Mandelbrot contained in the Mandelbar:

I really like the coloring of this one.

OK, so what if you're starting to get bored by Mandelbar too?  Let's try pumping them up a bit in our next blog.

December to Remember

When Winter Break came around this year, I had a good two-and-a-half or three weeks to get my relax on.  True, I had some goals to be "productive" during my time off (like, for example, finishing Chapter 4 in my novel).  However, I spent the first week of break playing solitaire online.  So much for productivity!

Finally, I had enough of my time wasting.  I decided that if I wasn't going to be productive, then I would have something to show for all time I was wasting.  I decided to try once again to program some fractals.

Instead of looking for C code, this time I searched out Java.  I found an applet that looked OK and had source code available.  I downloaded the source code but found important parts of it missing.  On top of that, I couldn't get my Java Virtual Machine to compile it or run it.

Fortunately, I was on Winter Break: I had tons of time to work on these issues.  The problem with Java is that my browser was hogging all the Java resources.  So now I browse Java-free (no more internet solitaire!), but I can run my own programs in Java whenever I want.

The second problem was when I discovered this Fractal Applet.  Created by a former Computer Science professor named David Leberknight, the applet is both an excellent implementation of the Mandelbrot Set as well as a perfect example of object-oriented programming.  In addition to all this, David graciously allows others to use the program if they give credit.  David, I raise my glass to you: Thank you!!

David provides explicit instructions on his download page.  I followed his instructions, turning the applet into a console application.  The next thing I did was to add the Save button.  This was easier than it sounded on the instruction page, and has allowed me to save the images I create.  Without the Save functionality, I wouldn't be doing this blog because there wouldn't be any visuals to go along with my explanations.

Besides David's instructions on how to use his applet/application, the structure of his code made it simple for me to improve.  Actually, improve is not quite the right word here.  I added things to the program, so I "improved" it in the sense that I made it do more things.  But I certainly didn't improve it in the sense of correcting what was wrong, streamlining it, or somehow making it better.  I didn't make it better, I only made it bigger.  Whatever, the point here is that it has been fairly simple for me to add new fractal classes to the code because he implemented the original program so well.

The one thing that continues to amaze me about David's program is how much you can zoom in on a fractal.  I've played with a number of fractal programs in my time, but David's is the fastest, especially when it comes to mega-magnification.  For example, here is a fractal that has been magnified many times.

This image displays one of the features that defines a fractal: self-similarity.  This tiny Mandelbrot Set (or "mini-me") resembles the original M-set but is so small that it is not visible when viewing the original set.  The blue tendrils in this image also exhibit self-similarity.  In fact, this shot was taken out of a much larger field that had similar tendrils of varying sizes all around.  It is the features of David's code that allows this unique shot to be seen.

There are three features in David's code that contributed to the uniqueness of the above shot. I've already mentioned the ability it has to zoom into small portions of the fractal.  The code also has several color schemes available (this happens to be the default, but you will see some of the other colors available if you keep reading my posts).  In addition, the program allows you to specify the number of iterations.

See, the Mandelbrot Set is an example of an "Escape Time" fractal.  What the computer does for each pixel is computes z = z^2 + c (that is, the new number is the square of the old number, plus the original pixel we started with).  This is all done on the complex plane.  Each time the value is calculated is called an "iteration."  After each iteration, the number is checked; if it is too large, then the calculations are stopped and the pixel is given a color, based on how quickly the number grew too large.  That's the "escape" part of the computational algorithm.

If the pixel never gets too large -- it never "escapes to infinity" -- then it remains black.  But the question is, how many times do you iterate before you give up and call it good?  This is the "time" part.  Without setting some upper bound (or limit) to the number of iterations, you would have an infinite loop -- worse, you would have no picture to look at.  Fractal artists have found there is a balance between the amount of detail your picture has and the time it takes to create the picture.

For example, here's the Mandelbrot Set at various iterations.

 This is 1 iteration.  It's just a circle of radius 3.  (That's the escape value I use.)

 This is 5 iterations.  It's starting to resemble the Mandelbrot shape.

 Here's 10 iterations.  A lot of definition is starting to become visible.

This is the fully formed Mandelbrot Set, at 33 iterations.  The red color, as well as the fine details, are both due to the additional iterations.

Lately, I have experimented with different iterations.  Initially, I started doing this to vary the colors in the picture, but I found that in certain detailed images, the image itself can vary widely.  For example, here's an animated gif I made from a tiny feature with iterations ranging from 250 to 600.  (You will probably have to click on the image to see the animation.  It's also kind of slowly animated, but it's well worth waiting for.)

I think what's happening here is that as the iterations increase, more and more pixels are "escaping" and fewer remain black.

So David's code allows one to explore in great detail the landscapes within the Mandelbrot Set.  The main reason I adopted and adapted David's code was so I could explore other fractals.  These other fractals are similar to Mandelbrot but have different equations.  Stay tuned as we explore some of these other equations.

3D Summer

There are many, many programs you can download that make fractals.  Most of them are free and most of them are easy to use.  I have barely scratched the surface of what is out there, so I don't feel like I can make a recommendation.  Since art is subjective, I'd suggest you find your own favorite through google and experimentation.

This past summer, however, a good friend and fellow geek shared the Mandelbox Zoom video on a well-known social networking site.  It blew my mind, and I'm sure it will blow yours, too.

 

Mandelbox Zoom from hömpörgő on Vimeo.

I couldn't believe the colors, the details.  I was amazed by the new yet familiar shapes, all in 3D.  And the video was like flying through this giant alien city (Coruscant, anyone?).  Turns out there's a program that generated the Mandelbox and created the "film."  It's called Mandelbulb3d and it's available at fractalforums.com.  I immediately downloaded it and started experimenting.  Check this out:

The software has functionality to string together a series of (zoomed) images.  It looks like a movie, but you can save it as an animated GIF, like this:

I've always enjoyed the Sierpinski gasket, and the Menger sponge, but I never considered the Sierpinski icosahedron:

As you can see, Mandelbulb3d has a number of fomulas you can display, in both 2D and 3D, and it lets you adjust some parameters as well as make Julia sets.  You can also rotate the three dimensional object.  One of the fomulas we will explore later is the Mandelbar formula, called "Tricorn" in Mandelbulb3d and displayed below.

It looks like a fighter spacecraft.  You can even see a cockpit area!

Frankly, most of the capabilities of Mandelbulb3d were above my head.  I don't understand some of the formulas (there's one for Quaternions, whatever those are).  I know nothing about 3D rendering so being able to adjust those various parameters meant nothing for me.  Nevertheless, my fractal urges were nearly satisfied, at least until Winter Break.

Programming Fractals Part One

Most people have short but frequent blocks of free time.  These are commonly called weekends.  They come once a week but one rarely has enough time to complete a major project.

However, I am currently a grad student.  That means my free time comes in large but very infrequent chunks, like Spring Break and Winter Break.  So what does a math geek with computer programming experience do on Spring Break?  Allow me to share what I did.

On one of the Internets, I found some C-code that painted interesting fractal pictures.  First, I had to get the code to work on my machine.  This required downloading a free copy of Visual C++.  (I know what you're thinking: Micro$oft gave away a free copy of their software?  I couldn't believe it either, and there have been no bad effects, either.)  The "readme" file with the code also suggested getting GIMP, so I did.

(GIMP is an acronym that stands for GNU Image Manipulation Program.  If you don't know GNU, think "open source."  Personally, I believe in open source software when I can't afford a program like Photoshop.  For my image manipulation needs and abilities, GIMP is more than adequate, and you can't beat the price.  It cost me as much as Visual C++ did.)

So then I was up and running.  It turned out that the code I downloaded created "buddhabrot" fractals.  These are basically Mandelbrot sets but with a totally different coloring algorithm.  Allow me to explain how it works: Click Here.  I'll wait.  Really, you want to read this, it's way cool.  What?  You'd rather read something quick and get back to this blog?  OK, here's Wikipedia.  All right, are you back?

Here is the buddhabrot I drew with the downloaded code.

Pretty cool, huh?  (You really should go back and read that first link by the creator of the buddhabrot.  Seriously, I'm not going to explain it to you.)

I love the other-worldly nature of this picture.  However, there were a couple things I wasn't crazy about.  The first, and not as important, was that it took a long time to create.  This is to be expected, since the buddhabrot algorithm takes twice as long anyway.  But you already know this because you read the links above.  I would have been happy to create buddhabrots while sleeping or something, so this wasn't that big a deal (until I came across something faster).

The second thing about my buddhabrot images was that they were simply images.  I can't zoom in closer to look at the internal structure.  That's one of the best things about Mandelbrot and other escape-time fractals: you can zoom in thousands of times and still see minute detail of the chaotic borders.  (More on that to come.)

But I was far from disappointed.  I was able to begin my fractal addiction by manipulating the equation that creates the fractal.  I'll explain the equations later. Allow me to close with the other buddhabrot-type images I created.  Next time: Summer Break!

          Cubic Mandelbrot

 

Quartic Mandelbrot

                                                                          Mandelbar    

Will Blog for Fractals

For years, I was mildly interested in fractals, especially the iterative kind.  But since I used to be a programmer, I always wanted to make my own fractals.  By "make" I don't mean use someone else's software and move the mouse around until you find a pretty picture.  Instead, I mean create some new equations, making new fractals for me and others to study and enjoy.  This blog now exists because I have finally succeeded in attaining my goal.

What follows will be a brief history of my fractalage, I mean, creation of fractals, in a handful of posts.  Since a picture is worth a thousand words, I will be sure to illustrate my posts.  Stay tuned, and soon we will be sharing some amazing fractals!

--mandelscott